
Zadanie Króliki (kro)
Pomóż nam usprawnić bazę zadań!
Króliki
Limit pamięci: 256 MB
Bajtazar postanowił zacząć żyć ekologicznie, i został hodowcą sałaty. Jak wiadomo, bajtockie króliki uwielbiają sałatę, nic więc dziwnego, że wkrótce zawitały one do ogródka Bajtazara.
Wokół domu Bajtazara rozmieszczone jest  grządek sałaty, które będziemy
numerować od
grządek sałaty, które będziemy
numerować od 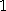 do
do  .
Każde dwie kolejne grządki sąsiadują ze sobą, tzn. dla każdego
.
Każde dwie kolejne grządki sąsiadują ze sobą, tzn. dla każdego 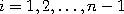 grządki o numerach
grządki o numerach 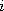 oraz
oraz 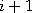 sąsiadują ze sobą.
Dodatkowo, grządka o numerze
sąsiadują ze sobą.
Dodatkowo, grządka o numerze  sąsiaduje z grządką o numerze
sąsiaduje z grządką o numerze 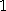 .
Na grządce o numerze
.
Na grządce o numerze 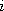 siedzi
siedzi 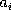 królików i pałaszuje sałatę Bajtazara.
królików i pałaszuje sałatę Bajtazara.
Bajtazar chciałby przegonić z ogródka jak najwięcej królików.
Ma do dyspozycji swoją starą, wierną strzelbę, w której jest 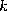 nabojów.
Króliki są bardzo płochliwe, więc gdy tylko Bajtazar wystrzeli
w kierunku grządki o numerze
nabojów.
Króliki są bardzo płochliwe, więc gdy tylko Bajtazar wystrzeli
w kierunku grządki o numerze 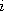 , to wszystkie króliki z tej grządki
uciekają w siną dal.
Co więcej, przestraszone króliki z obu sąsiednich grządek
przeskakują na dalsze grządki, tzn. kicają na grządkę sąsiadującą
z tą, na której stoją - oczywiście nie tą, w kierunku której strzelał Bajtazar.
, to wszystkie króliki z tej grządki
uciekają w siną dal.
Co więcej, przestraszone króliki z obu sąsiednich grządek
przeskakują na dalsze grządki, tzn. kicają na grządkę sąsiadującą
z tą, na której stoją - oczywiście nie tą, w kierunku której strzelał Bajtazar.
Pomóż Bajtazarowi i wyznacz maksymalną liczbę królików, które może on
wygonić z ogródka za pomocą co najwyżej 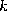 strzałów.
strzałów.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite
 i
i 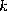 (
(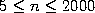 ,
, 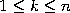 ),
oznaczające liczbę grządek w ogródku i liczbę nabojów w strzelbie Bajtazara.
W drugim wierszu znajduje się ciąg liczb całkowitych
),
oznaczające liczbę grządek w ogródku i liczbę nabojów w strzelbie Bajtazara.
W drugim wierszu znajduje się ciąg liczb całkowitych 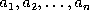 (
(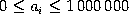 ), które oznaczają liczby królików
na kolejnych grządkach.
), które oznaczają liczby królików
na kolejnych grządkach.
Wyjście
Na wyjście należy wypisać jedną liczbę całkowitą - maksymalną liczbę królików, które Bajtazar jest w stanie przegonić z ogródka.
Przykład
Dla danych wejściowych:
5 2 6 1 5 3 4
poprawną odpowiedzią jest:
13
Wyjaśnienie do przykładu: Bajtazar przegania 6 królików z grządki numer 1 (wskutek czego króliki z grządki numer 5 przeskakują na grządkę numer 4, zaś króliki z grządki numer 2 przeskakują na grządkę numer 3), a następnie przegania 7 królików z grządki numer 4.
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English